Rubyistのための機械学習入門

k-means(k平均法, k-means clustering)とは?

与えられたデータを元に複数のグループ(クラスタ)に分割する手法です

教師なし学習の一種
与えられた m 個のデータを元にデータを k 個の非階層クラスタに分類

顧客のセグメント分類などに応用が可能です

k(=2) 個のクラスタに分類する例

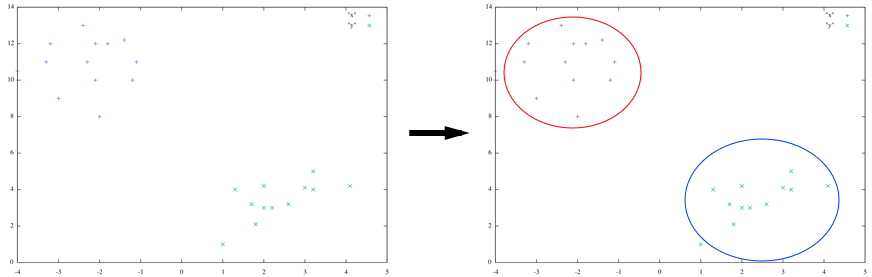
クラスタリングの例

顧客分析で性別, 生年月日, 過去Xヶ月の購入金額, 過去1年の訪問回数, 曜日別の訪問回数… など多数の顧客データがあった場合でも容易にクラスタ分割ができます

アルゴリズム

アルゴリズムは非常に単純です

必要な入力

分類したいクラスタ数(k)
データセット

学習ステップ

1. クラスタの初期重心の選択

ランダムに k 個の点を選びます

データセットから k個ユニークなデータを選択し、それを初期重心とします

2. 各データをラベル付け

各データをクラスタの重心に近いほうにラベル付け

様々な手法がありますが、簡単に計算できるユークリッド距離を利用します

E.g.)

重心: 点A(1, 3), 点B(10, 8) データ: (3, 2)

このデータと重心Aとの距離は

√((1 - 3) ^ 2 + (3 - 2) ^ 2) = √4

このデータと重心Bとの距離は

√((10 - 3) ^ 2 + (8 - 2) ^ 2) = √85

数値が小さいほうが距離が近いことになるので、このデータの場合は重心A にラベル付されます
※実際の実装においては平方根の計算をしてもしなくても、距離の大小関係はわかるため、平方根の計算はしません

3. 重心の移動

でラベル付けされたデータの平均値の箇所に重心を移動させます

E.g.)
クラスタAとラベル付けされたデータセット

[ (1, 3), (2, 3), (1, 2) ]

平均値はそれぞれ

X座標: ( 1 + 2 + 1) / 3 = 4/3
Y座標: ( 3 + 3 + 2) / 3 = 8/3

であるので、

クラスタAの重心は(4/3, 8/3)となります

4. 繰り返し

2., 3. を重心が(ほとんど)移動しなくなるまでまたは学習を指定回数分繰り返したところで終了します

問題点

k-means法では、初期の重心の選択方法によって結果が局所解に陥ります

よい重心が選択された例

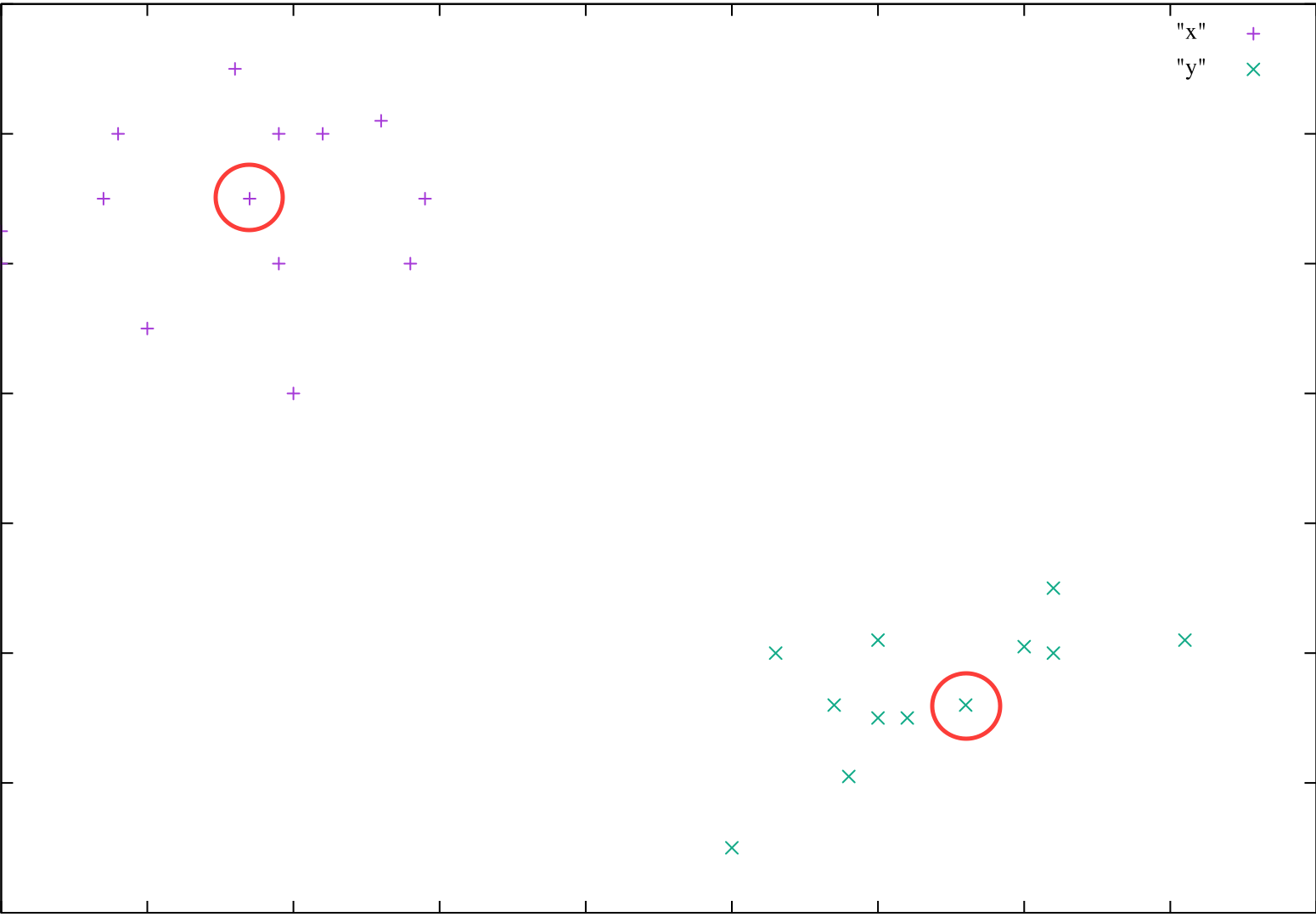
良い重心選択

悪い重心が選択された例

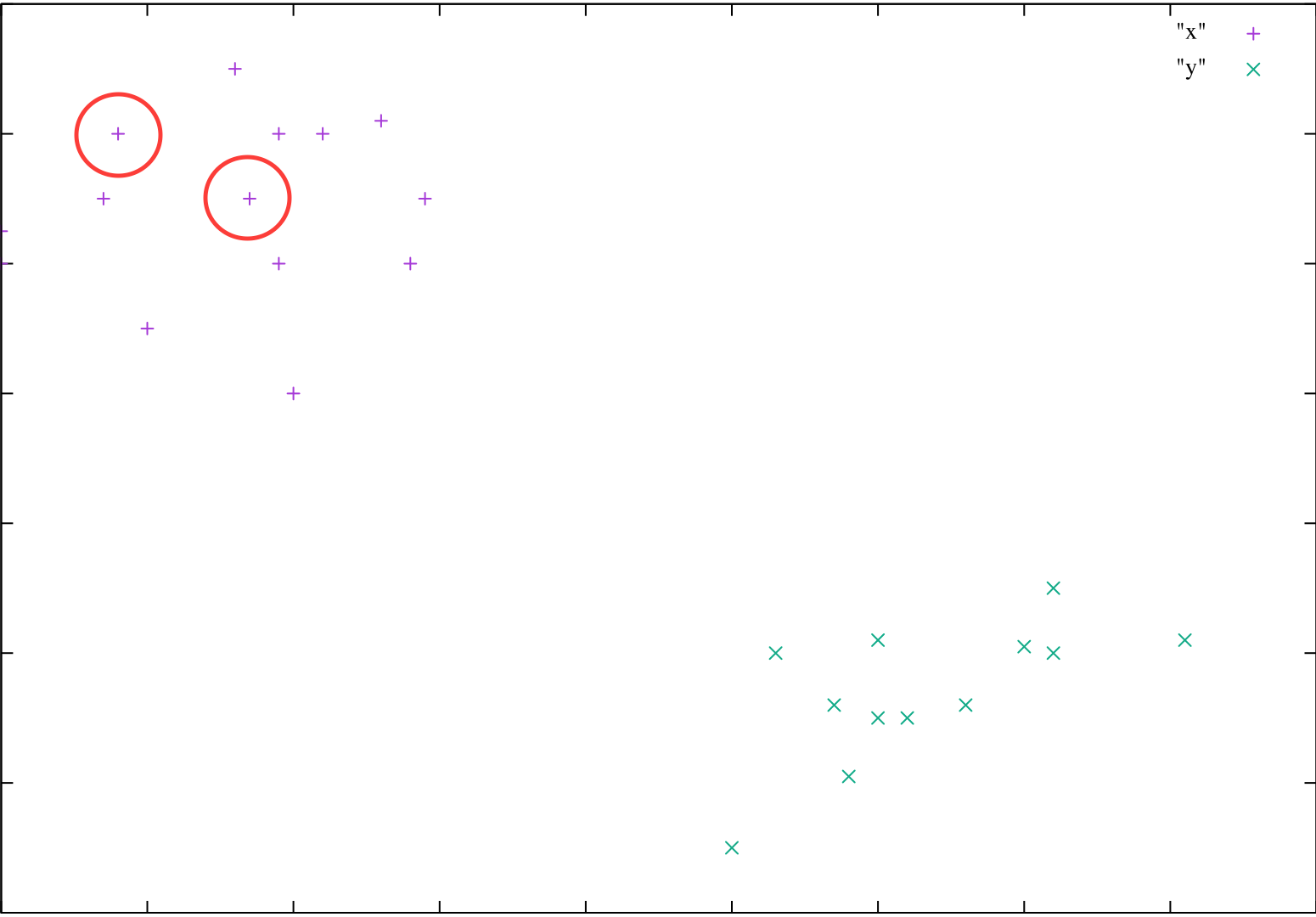
悪い重心選択

目視でみると、左上、右下の2グループに分類されそうなことがわかります
しかし、悪い重心が選択された場合には初期の重心の位置から分類が始まってしまうため、
異なった分類がされてしまいます

解決方法

k-means++法(Wikipedia) という方法で回避できます
また、単純に重心の初期化を何度も繰り返すという方法でも回避できます
今回の実装はこの重心の初期化を何度も繰り返すという方法で実装しています
もちろん、計算量が多くなるため、k-means++法を用いるほうが良いです

初期化を繰り返し、最適値を見つけるアルゴリズム

クラスタの初期重心の選択
各データをラベル付け
重心の移動
データのラベル付け、重心の移動を繰り返す
コストの計算

上記を繰り返し、最もコストが低くなったデータの重心を採用します

具体的なRubyでの実装

※適当につくったやつなのでバグがあったらごめんなさい

Repository: learning_k_means

データセット

各都道府県の総人口と各年代の構成比率(2014年10月時点)をcsvにしたものを用います

なお、e-Statをデータの元データとして利用しています

http://www.e-stat.go.jp/SG1/estat/List.do?lid=000001132435

実行方法

チェックアウト後に bin/population を実行してみてください

$ bin/population -c 3 -t 100
centroid 0: Vector[501/2875, 9657/115000, 5197/46000, 14469/115000, 3689/28750, 8899/57500, 13723/115000, 2313/23000]
centroid 1: Vector[6487/35000, 7803/70000, 9503/70000, 10761/70000, 4149/35000, 9167/70000, 1027/10000, 2151/35000]
centroid 2: Vector[3019/17000, 16759/170000, 259/2125, 703/5000, 10359/85000, 12549/85000, 4801/42500, 1677/21250]
cost: 0.017160089426379248

※ -c: クラスタ数
※ -t: 重心の初期化の繰り返し回数

大体以下のように分類されます

クラスタA	クラスタB	クラスタC
青森県岩手県秋田県山形県福島県新潟県富山県福井県長野県和歌山県鳥取県島根県山口県徳島県香川県愛媛県高知県佐賀県長崎県熊本県大分県宮崎県鹿児島県	埼玉県東京都神奈川県愛知県滋賀県大阪府沖縄県	北海道宮城県茨城県栃木県群馬県千葉県石川県山梨県岐阜県静岡県三重県京都府兵庫県奈良県岡山県広島県福岡県

興味深いのは、この分類の仕方の場合
東京都、神奈川県などのThe都会のチームに滋賀県、沖縄県が含まれていることですね

詳細なRubyプログラムの解説

メイン処理

session#train がメイン処理です

# lib/learning_k_means/session#train

def train(step = 5)
  # 初期重心の選択
  @centroids = initialize_centroids

  cluster_items = nil

  # step数分重心の移動を繰り返す
  0.upto(step) do |i|
    # データセットのラベル付け
    cluster_items = assign_cluster(@dataset, @centroids)
    # クラスタ重心の移動
    @centroids = move_centorids(cluster_items)
  end
  # 学習後のコストを返す
  compute_cost(cluster_items, @centroids)
end

重心の初期化(initialize_centroids)

重心をランダムに初期化する処理です

ここで distinct_int_value は 0 から @dataset.size の中から @cluster_size分ユニークな数値を選択するメソッドです E.g.) @dataset.size = 10, @cluster_size = 3 の場合 [1, 3, 2] や [2, 6, 8]などの数値が選択されますただし、[1, 1, 2] のように重複した数値は選択されません

# lib/learning_k_means/session#initialize_centroids

def initialize_centroids
  [].tap do |centroids|
    distinct_int_value(@cluster_size, @dataset.size).each do |index|
      centroids << @dataset[index]
    end
  end
end

※@dataset は元データの配列を示します ※@cluster_size は分類したいクラスタの個数 k を示します

データセットのラベル付け

現在の重心に対して、近い方にラベル付していきます

# lib/learning_k_means/session#assign_cluster

def assign_cluster(dataset, centroids)
  {}.tap do |cluster_items|
    dataset.each_with_index do |vector, i|
      cluster_index = select_cluster(vector, centroids)
      cluster_items[cluster_index] ||= []
      cluster_items[cluster_index] << vector
    end
  end
end

結果は各クラスタのindexをキーとし、内部に含まれるデータセットの配列の形式で返ります

E.g.) k = 3 の場合

{
  1: [Vector, Vector, Vector, ...]
  2: [Vector, Vector, ...]
  3: [Vector, Vector, Vector, Vector, ...]
}

ここで select_cluster は vector は与えられた重心k個のどれに近いのかを返す関数です

重心の移動

各クラスタに含まれている要素の平均をクラスタの重心として返します

# lib/learning_k_means/session#move_centorids

def move_centorids(cluster_items)
  [].tap do |o|
    cluster_items.each_pair do |cluster_index, items|
      o[cluster_index] = items.inject(:+) / items.size
    end
  end
end

※itemsは Vector の配列です

items.inject(:+) / items.size は以下のような結果になります

require 'matrix'

x = [Vector[1, 2, 3], Vector[2, 4, 5]]

x.inject(:+)
# => Vector[3, 6, 8]

x.inject(:+) / x.size
# => Vector[1, 3, 4]

コストの計算

各クラスタ単位でラベル付けされたデータセットの各点と重心の距離の合計をコストの値としています

# lib/learning_k_means/session#compute_cost
def compute_cost(cluster_items, centroids)
  [].tap do |cost|
    cluster_items.each do |cluster_index, items|
      cost[cluster_index] = items.map {|item| norm_square(item, centroids[cluster_index]) }.inject(:+)
    end
  end.inject(:+)
end

E.g.
1回目
クラスタA: { (3, 5), (-2, 4) }
クラスタAの重心: (2, 3)

この場合コストは ( 2 - 3 ) ^ 2 + ( 3 - 5 ) ^ 2 + ( 2 - (-2) ) ^2 + ( 3 - 4 ) ^ 2 = 22

2回目
クラスタA: [ (1, 2), (3, 4) ]
クラスタAの重心: (2, 1)

この場合コストは ( 2 - 1 ) ^ 2 + ( 1 - 2 ) ^ 2 + ( 2 - 3 ) ^2 + ( 1 - 4 ) ^ 2 = 12

となり、2回目のほうがコストが低くなるため、2回目で選択された重心を採用することになります

Rubyistのための機械学習入門 - k-means編